
全部
▼
搜索
熱搜:
位置:中冶有色 >
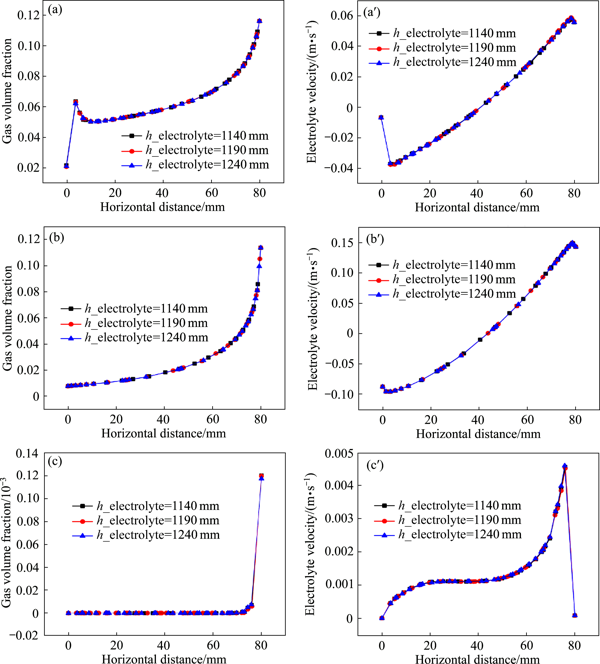
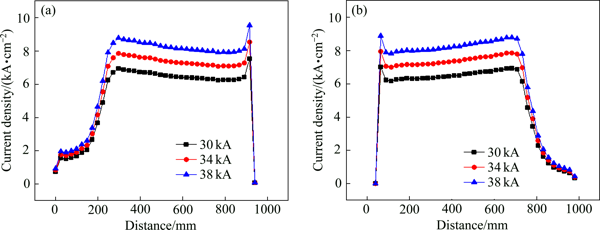
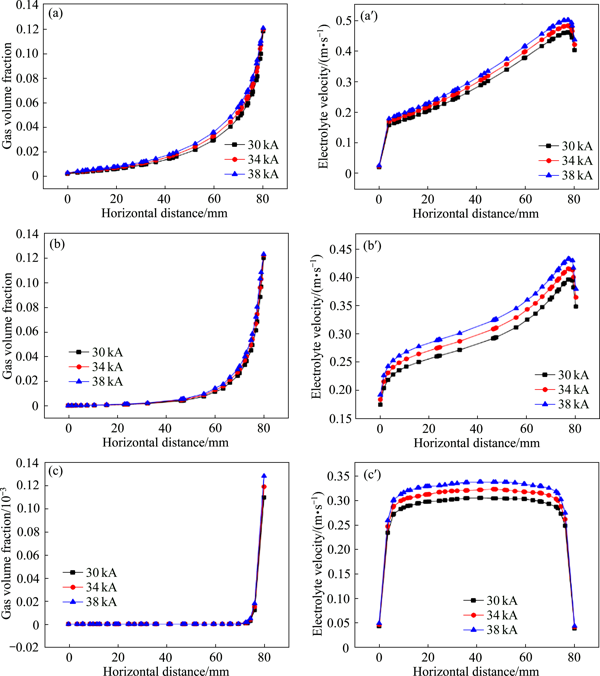
> 鋰電解槽極間通道內(nèi)兩相流場數(shù)值模擬
 976
編輯:中冶有色技術(shù)網(wǎng)
來源:李文英,吳荔荔,路貴民
976
編輯:中冶有色技術(shù)網(wǎng)
來源:李文英,吳荔荔,路貴民



 分享 0
分享 0
 舉報(bào) 0
舉報(bào) 0
 收藏 0
收藏 0
 反對 0
反對 0
 點(diǎn)贊 0
點(diǎn)贊 0

 中冶有色技術(shù)平臺(tái)
中冶有色技術(shù)平臺(tái) 2025年03月25日 ~ 27日
2025年03月25日 ~ 27日  2025年03月28日 ~ 30日
2025年03月28日 ~ 30日  2025年03月28日 ~ 30日
2025年03月28日 ~ 30日  2025年03月28日 ~ 30日
2025年03月28日 ~ 30日  2025年04月27日 ~ 29日
2025年04月27日 ~ 29日 
