
全部
▼
搜索
熱搜:
位置:中冶有色 >
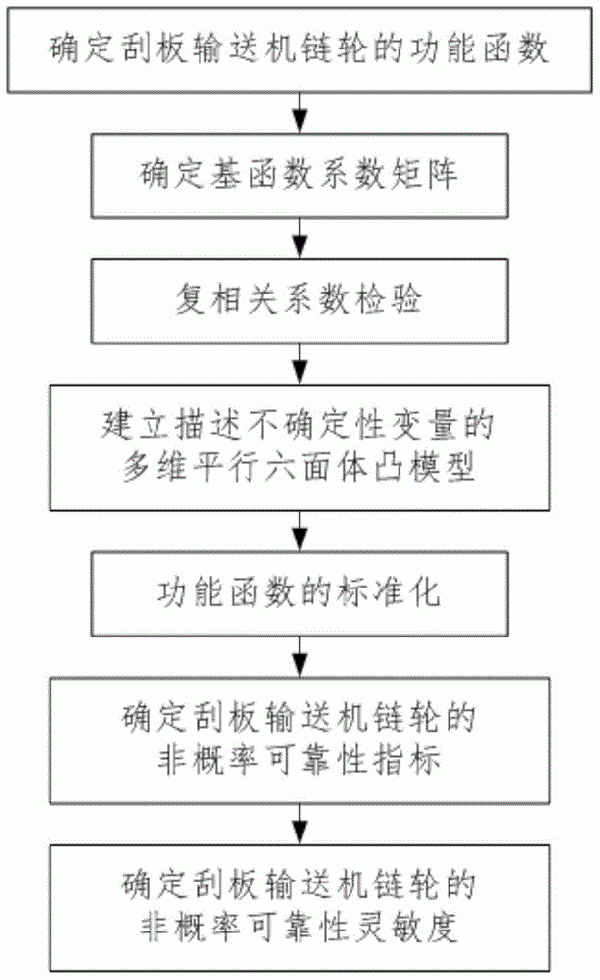
> 刮板輸送機鏈輪的非概率可靠性靈敏度分析方法
 493
編輯:中冶有色技術(shù)網(wǎng)
來源:西安科技大學(xué)
493
編輯:中冶有色技術(shù)網(wǎng)
來源:西安科技大學(xué)
 分享 0
分享 0
 舉報 0
舉報 0
 收藏 0
收藏 0
 反對 0
反對 0
 點贊 0
點贊 0

 中冶有色技術(shù)平臺
中冶有色技術(shù)平臺 2025年03月21日 ~ 23日
2025年03月21日 ~ 23日  2025年03月28日 ~ 30日
2025年03月28日 ~ 30日  2025年04月11日 ~ 13日
2025年04月11日 ~ 13日  2025年04月11日 ~ 13日
2025年04月11日 ~ 13日  2025年04月24日 ~ 27日
2025年04月24日 ~ 27日 
