
全部
▼
搜索
熱搜:
位置:中冶有色 >
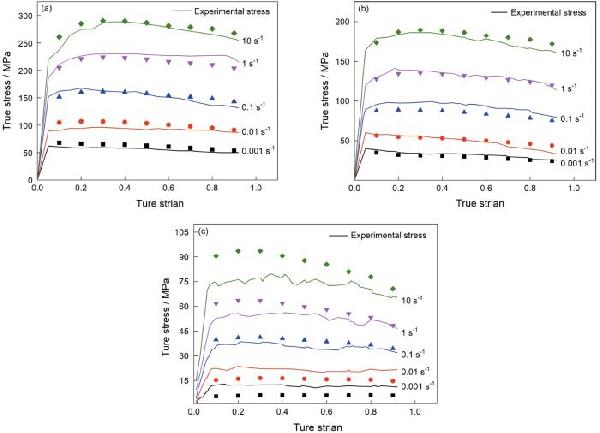
> TA5鈦合金的應(yīng)變補償物理本構(gòu)模型和加工圖
 555
編輯:中冶有色技術(shù)網(wǎng)
來源:王俊,王克魯,魯世強,李鑫,歐陽德來,邱仟,高鑫,張開銘
555
編輯:中冶有色技術(shù)網(wǎng)
來源:王俊,王克魯,魯世強,李鑫,歐陽德來,邱仟,高鑫,張開銘

|
D0/ m2·s-1 |
Qsd/ J·mol-1 |
G0/ MPa |
E0/ GPa |
Tm/ K |
TmG0dGdT |
|---|---|---|---|---|---|
| 1.5×10-4 | 2.91×105 | 4.36×104 | 126 | 1933 | -1.2 |



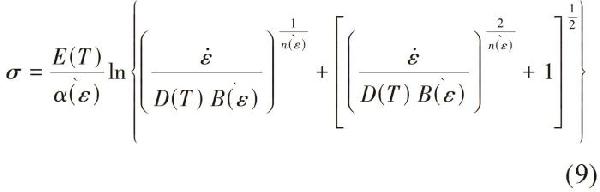

 分享 0
分享 0
 舉報 0
舉報 0
 收藏 0
收藏 0
 反對 0
反對 0
 點贊 0
點贊 0

 中冶有色技術(shù)平臺
中冶有色技術(shù)平臺 2025年03月25日 ~ 27日
2025年03月25日 ~ 27日  2025年03月28日 ~ 30日
2025年03月28日 ~ 30日  2025年03月29日 ~ 31日
2025年03月29日 ~ 31日  2025年04月11日 ~ 13日
2025年04月11日 ~ 13日  2025年04月11日 ~ 13日
2025年04月11日 ~ 13日 
