液晶(Liquid crystal, LC)的性狀介于液態(tài)與固態(tài)之間,既具有液體的流動(dòng)性,又具有晶體的各向異性 液晶的場(chǎng)效應(yīng)、雙折射特性以及對(duì)溫度的靈敏性使其可應(yīng)用于液晶顯示器(Liquid crystal display, LCD)、空間光調(diào)制器(Liquid crystal spatial light modulator, LCSLM)[1]、傳感器[2]等器件 用于液晶顯示的液晶多為向列相液晶(Nematic liquid crystals, NLC) 向列相液晶[3]分子呈長(zhǎng)棒狀,長(zhǎng)徑比大于4,結(jié)構(gòu)中含有由苯環(huán)或環(huán)己烷組成的堅(jiān)硬部分和由碳鏈組成的柔軟部分,在無(wú)外加場(chǎng)或邊界條件時(shí)沿長(zhǎng)軸彼此平行排列,具有長(zhǎng)程取向序 液晶對(duì)外場(chǎng)非常靈敏的響應(yīng),使其在顯示領(lǐng)域占有主導(dǎo)地位 在電場(chǎng)中,液晶分子受到傾向于轉(zhuǎn)向沿電場(chǎng)方向或垂直于電場(chǎng)方向的轉(zhuǎn)矩,而自身又存在由邊界條件限制而引起的自身形變轉(zhuǎn)矩,二者在平衡條件下可以相互抵消,故只有外場(chǎng)強(qiáng)度超過一定閾值時(shí)液晶內(nèi)部的分子才傾向于轉(zhuǎn)向與外場(chǎng)平行或垂直的方向排列,即發(fā)生Freedericksz轉(zhuǎn)變 例如,扭曲向列型(Twisted nematic, TN)液晶顯示正是基于液晶分子的扭曲與Freedericksz轉(zhuǎn)變,施加驅(qū)動(dòng)電壓、調(diào)制透光率可實(shí)現(xiàn)黑白或彩色顯示 閾值電壓描述液晶分子排列發(fā)生轉(zhuǎn)變的臨界電壓,是評(píng)價(jià)液晶器件能耗的重要參數(shù),降低閾值電壓可面向節(jié)能電光設(shè)備的應(yīng)用；響應(yīng)時(shí)間描述液晶分子在所施加電壓下發(fā)生偏轉(zhuǎn)的響應(yīng)速度,也是評(píng)價(jià)液晶器件的重要參數(shù) 提高響應(yīng)速度、降低響應(yīng)時(shí)間,可改善圖像拖影、實(shí)現(xiàn)高幀率驅(qū)動(dòng)

目前LCD產(chǎn)業(yè)的發(fā)展受阻 與有機(jī)發(fā)光二極管(Organic light emitting diode, OLED)等新型發(fā)光材料相比,LCD有刷新率低、色域窄、厚度大等不足 基于電子競(jìng)技對(duì)顯示刷新率的要求,頂級(jí)電競(jìng)顯示器不得不考慮選用價(jià)格昂貴的OLED面板 提高液晶材料分子的響應(yīng)速度、降低響應(yīng)時(shí)間,可提高IPS(In-plane switching)面板的刷新率,提高液晶材料的市場(chǎng)競(jìng)爭(zhēng)力 在實(shí)際應(yīng)用中,常將多種單體液晶混合配制混晶或向液晶中摻入納米粒子[4]以克服液晶單體清亮點(diǎn)較低、驅(qū)動(dòng)電壓過高、粘度太大等不利因素以優(yōu)化顯示性能,或在液晶中摻入同具棒狀結(jié)構(gòu)和取向液晶態(tài)的納米材料以得到需要的性能參數(shù)

碳納米管(Carbon nanotubes, CNTs)具有棒狀幾何外形,其長(zhǎng)徑比為液晶分子長(zhǎng)徑比的數(shù)十至數(shù)百倍,使碳納米管具有更優(yōu)的電光各向異性 將碳納米管與液晶結(jié)合可實(shí)現(xiàn)優(yōu)勢(shì)互補(bǔ),增大復(fù)合體系的介電各向異性[5~7] 同時(shí),高濃度碳納米管分散液可呈現(xiàn)有序取向液晶態(tài),再現(xiàn)液晶科學(xué)中的各種缺陷行為,預(yù)示著碳納米管與液晶之間的取向相似性[8]；若與液晶結(jié)合可優(yōu)化二者的有序取向性,進(jìn)而優(yōu)化復(fù)合體系的電、光等物理性質(zhì)

同時(shí),碳納米管六元環(huán)結(jié)構(gòu)中的碳原子具有sp2雜化狀態(tài),其中雙鍵中未雜化的p軌道在垂直于環(huán)平面方向上彼此交疊、形成高度離域化的大π鍵 碳納米管壁外的離域π鍵是其與一些具有共軛性能的分子以非共價(jià)鍵復(fù)合的化學(xué)基礎(chǔ) 而液晶分子的堅(jiān)硬部分也含有由苯環(huán)結(jié)構(gòu)形成的共軛體系,且有些液晶分子的柔軟部分還包含有單雙鍵交替的共軛結(jié)構(gòu) 這表明,碳納米管與液晶分子之間可通過π-π相互作用形成穩(wěn)定的復(fù)合體系,實(shí)現(xiàn)二者優(yōu)勢(shì)互補(bǔ)以改善顯示材料的電光性能

Yuqiang等[9]研究表明,在各種頻率下多孔結(jié)構(gòu)多壁碳納米管的摻入會(huì)增大NLC的電容,影響液晶的閾值電壓和介電性質(zhì)；而De Filpo等[10]的研究表明,高長(zhǎng)徑比單壁碳納米管可呈纖維狀、沿指向矢排列,增大電導(dǎo)率和降低重定向場(chǎng),因此即使微量摻入也有利于大幅降低液晶的閾值電壓、驅(qū)動(dòng)電壓 Singh D等[11]發(fā)現(xiàn),將單壁碳納米管摻入NLC可使其閾值電壓降低20%~30%,介電各向異性也有所提高 這表明,將碳納米管與液晶復(fù)合有望增強(qiáng)液晶顯示單元中液晶/碳納米管復(fù)合體的取向有序性、改變器件工作閾值電壓、提高材料的響應(yīng)速度,從而提高LCD的顯示性能

4"-正戊基-4-氰基聯(lián)苯(4-cyano-4’-pentylbiphenyl, 5CB)液晶作為一種常用的溶劑型液晶,是混晶的組成成分,其因結(jié)構(gòu)中的兩個(gè)苯環(huán)具有與碳納米管產(chǎn)生π-π相互作用的潛在位點(diǎn),故5CB液晶是探索其與納米材料復(fù)合的首選[12] 同時(shí),考慮苯基、乙烯基與碳納米管間的π-π相互作用[13],選擇柔軟部分帶雙鍵的4-[反式-4-[(E)-1-丙烯基]環(huán)己基]苯腈(4-[trans-4-[(E)-1-Propenyl]cyclohexyl]benzonitrile,記為16CN)與5CB混合配制混晶,選擇兩種液晶作為對(duì)比,以評(píng)估適合與碳納米管復(fù)合的液晶所具有的結(jié)構(gòu)特點(diǎn)

本文在5CB單晶及5CB液晶與所選烯類固態(tài)單晶的混晶中摻入碳納米管,基于液晶顯示單元——液晶盒的電容模型,用阻抗分析儀測(cè)試其電容-電壓曲線,分析給出顯示單元的閾值電壓,從而給出與其相關(guān)的復(fù)合體系的介電各向異性、彈性常數(shù)；測(cè)試低頻下的透光率-時(shí)間曲線給出顯示單元的響應(yīng)時(shí)間,從而給出與其相關(guān)的復(fù)合體系的粘滯系數(shù) 其測(cè)試與計(jì)算流程如圖1所示 同時(shí),基于廣義梯度近似下的密度泛函計(jì)算,給出碳納米管與液晶分子之間的相互作用機(jī)制,以佐證實(shí)驗(yàn)中碳納米管/液晶復(fù)合體系的行為

圖1



圖1實(shí)驗(yàn)測(cè)試與計(jì)算參數(shù)關(guān)聯(lián)圖

Fig.1Correlation diagram of experimental test and calculation parameters

1 理論基礎(chǔ)1.1 閾值電壓

選擇平行排列液晶盒(平行盒)測(cè)試閾值電壓,平行盒上下基板取向?qū)拥哪Σ练较蛳嗷テ叫?且預(yù)傾角為銳角；灌裝NLC的平行盒的閾值電壓只取決于展曲彈性常數(shù)k11,能很好地反應(yīng)所摻碳納米管對(duì)原液晶材料的影響 根據(jù)在電場(chǎng)作用下平行盒中液晶分子發(fā)生Freedericksz轉(zhuǎn)變的臨界分析,其閾值電壓[11]可表示為

πVth=πk11ε0Δε

(1)

其中k11為展曲彈性常數(shù),Δε為介電各向異性,ε0為真空介電常數(shù)

由此可見,平行盒的閾值電壓與展曲彈性常數(shù)k11、介電各向異性Δε密切相關(guān)；若已知閾值電壓與介電各向異性,可得到材料的展曲彈性常數(shù)k11

1.2 響應(yīng)時(shí)間

響應(yīng)時(shí)間描述體系分子在所施加電壓下發(fā)生偏轉(zhuǎn)的響應(yīng)速度,根據(jù)在所施加電壓下透過光強(qiáng)隨時(shí)間的變化曲線可獲知體系分子響應(yīng)外場(chǎng)的響應(yīng)時(shí)間 響應(yīng)時(shí)間包括上升時(shí)間(τon),即加電壓過程,透光率由90%變化到10%所需的時(shí)間,其表達(dá)式為

πτon=γ1d2ε0ΔεV2-Kiiπ2

(2)

下降時(shí)間(τoff),即去電壓過程,透光率由10%變化回90%所需的時(shí)間[14],其表達(dá)式為[15]

πτoff=γ1d2Kiiπ2

(3)

式中 γ1為液晶材料的轉(zhuǎn)動(dòng)粘滯系數(shù),d為液晶盒的盒厚,Kii為彈性常數(shù),V為所施加的電壓

由此可見,響應(yīng)上升時(shí)間與介電各向異性、彈性常數(shù)、粘滯系數(shù)以及所施加電壓相關(guān),而響應(yīng)下降時(shí)間只取決于粘滯系數(shù)與彈性常數(shù),因此實(shí)驗(yàn)中選擇用響應(yīng)下降時(shí)間計(jì)算粘滯系數(shù) 對(duì)于所選的平行液晶盒,式中的彈性常數(shù)為展曲彈性常數(shù)k11

1.3 基于密度泛函理論的第一性原理

第一性原理即應(yīng)用量子力學(xué)基本原理、采用將原子核與電子運(yùn)動(dòng)分開處理的玻恩-奧本海默(Born-Oppenheimer, BO)近似直接求解薛定諤方程,其中沒有實(shí)驗(yàn)的、經(jīng)驗(yàn)的或者半經(jīng)驗(yàn)的參量,有很好的移植性 密度泛函理論依據(jù)量子力學(xué)體系能量唯一由其電子密度決定、將薛定諤方程中復(fù)雜的波函數(shù)以電子密度泛函代替,從而建立方程、得到體系電子密度與能量 基于密度泛函理論的第一性原理可簡(jiǎn)化體系電子結(jié)構(gòu)計(jì)算,使研究大分子系統(tǒng)成為可能

2 實(shí)驗(yàn)方法2.1 實(shí)驗(yàn)用材料和設(shè)備

實(shí)驗(yàn)用材料：5CB液晶(純度≥99.8%),常溫下為乳白色、粘稠狀的溶劑型正性單晶,熔點(diǎn)為22.7℃,清亮點(diǎn)為35.5℃,其結(jié)構(gòu)式如圖2a所示；16CN(純度≥99.8%)常溫下為白色或類白色的固態(tài)正性單晶,熔點(diǎn)為66℃,清亮點(diǎn)為74.5℃,其結(jié)構(gòu)式如圖2b所示

圖2



圖2液晶分子的結(jié)構(gòu)

Fig.2Liquid crystal molecular structure

平行液晶盒的盒厚為4 μm,預(yù)傾角為1°；垂直液晶盒的盒厚為4 μm,預(yù)傾角為89°

多壁碳納米管的直徑為30~50 nm,長(zhǎng)度為10~20 μm,純度>95%

實(shí)驗(yàn)用設(shè)備：TH2838H型阻抗分析儀、AFG2000型信號(hào)發(fā)生器、UPO3102CS型數(shù)字熒光示波器以及He-Ne激光器(波長(zhǎng)為633 nm)、PDA36A2型硅探測(cè)器(波長(zhǎng)范圍為350~1100 nm,帶寬為12 MHz,晶體管主動(dòng)區(qū)為13 mm)

2.2 CNTs/LC復(fù)合制備

先將1.5 g5CB和0.3 g16CN混合并持續(xù)攪拌至充分溶解,制得混晶5CB/16CN(記為Mixed LC) 然后將30 mg碳納米管放入200 mL乙醇溶液中,用鈦合金探頭超聲破碎12 h后進(jìn)行梯度離心、過濾和干燥,制得長(zhǎng)度均勻的短碳納米管 最后,將0.01 g預(yù)處理碳納米管放入15 mL丙酮溶液中并超聲分散[16] 將15 μL和75 μL分散液依次加入到1 g的5CB和混晶中,用超聲混合直至丙酮揮發(fā)完全和碳納米管充分分散,制得碳納米管摻雜濃度分別為0.001%和0.005%的復(fù)合液晶體系

將復(fù)合液晶體系分別灌入平行液晶盒和垂直液晶盒中用紫外固化膠封口后備用

2.3 顯示參數(shù)的測(cè)試2.3.1 閾值電壓的測(cè)試

使用阻抗分析儀測(cè)試圖3所示灌注液晶的液晶盒 圖3中的阻抗分析儀連接計(jì)算機(jī),電極穿過烘箱夾在液晶盒兩極,烘箱溫度設(shè)置為25℃以保證測(cè)試在恒溫下進(jìn)行 測(cè)試時(shí)交流信號(hào)的頻率為1 kHz,電壓范圍為0~20 V 根據(jù)所得電容-電壓(C-V)曲線,采用切線法、尋找斜率最大切線的橫截距給出閾值電壓[17]；并基于平行盒在低電平下的電容值與垂直盒在高電平下的電容值,采用雙電容法由

εP=C2-VANL2-PAN1-sin21°Sε0sin289°-sin21°-C2-PANL2-PAN1-sin289°Sε0sin289°-sin21°

(4)

εV=C2-PANL2-PANsin289°-C2-VANL2-VANsin21°Sε0sin289°-sin21°

(5)

給出所灌注液晶材料的介電各向異性[18] 式中εP為液晶材料的平行介電常數(shù),εV為液晶材料的垂直介電常數(shù),C2-PAN為平行盒液晶層電容,C2-VAN為垂直盒液晶層電容,L2-PAN為平行盒液晶層厚度,L2-VAN為垂直盒液晶層厚度,S為基板有效電極面積

圖3



圖3阻抗分析儀測(cè)試系統(tǒng)

Fig.3Impedance analyzer test system

2.3.2 響應(yīng)時(shí)間的測(cè)試

基于液晶的場(chǎng)效應(yīng)行為,使用圖4所示的電光測(cè)試系統(tǒng),測(cè)試所選平行液晶盒的響應(yīng)時(shí)間 圖中,由激光源出射的激光依次正入射至偏振片A、液晶盒、偏振片B進(jìn)入探測(cè)器,經(jīng)數(shù)字示波器顯示反映偏振光經(jīng)平行液晶盒后透光率隨時(shí)間變化的曲線 其中的前后偏振片正交,并基于

圖4



圖4光電測(cè)試系統(tǒng)

Fig.4Opto-electronic test system

πT=sin2Δndπλsin22Ω

(6)

調(diào)制前偏振片的偏振化方向與平行液晶盒的前摩擦取向方向的夾角為45o,以使出射光強(qiáng)的明暗對(duì)比度最大 式中T為出射光強(qiáng),λ為激光源出射激光的波長(zhǎng),Δn為折射率各向異性,Ω為前偏振片A的偏振化方向與液晶盒的前摩擦取向方向夾角

測(cè)試時(shí)選擇頻率為1 Hz、峰峰值為1.8 V的類方波式信號(hào)(圖5)以降低內(nèi)部電場(chǎng)的影響,從而得到反映透光率隨時(shí)間動(dòng)態(tài)變化的曲線[19] 圖中方波部分為1 kHz的高頻脈沖信號(hào)

圖5



圖5頻率為1 kHz、峰峰值為1.8 V的類方波信號(hào)

Fig.5Square wave like signal with a frequency of 1 kHz and a peak-to-peak value of 1.8 V

2.3.3 基于密度泛函理論的第一性原理計(jì)算

基于密度泛函理論的第一性原理方法,采用廣義梯度近似(Generalized gradient approximation, GGA)[20]的交換關(guān)聯(lián)泛函經(jīng)Tkatchenko-Scheffler色散矯正,對(duì)CNT、5CB、16CN以及CNT/5CB、CNT/16CN等體系結(jié)構(gòu)進(jìn)行幾何優(yōu)化和計(jì)算最穩(wěn)定的能量 計(jì)算使用了全電子密度以及超精細(xì)網(wǎng)格精度,其自洽場(chǎng)收斂域?yàn)?0-6a.u. 所構(gòu)建的碳納米管為鋸齒型單壁碳納米管(8,0),管兩端加氫,直徑為0.6345 nm,管長(zhǎng)為2.205 nm

3 結(jié)果和討論3.1 CNTs的形貌

圖6給出了原樣碳納米管與預(yù)處理碳納米管的SEM照片 可以看出,原樣碳納米管長(zhǎng)度分散在數(shù)百納米到數(shù)十微米之間,長(zhǎng)短不一且相差懸殊；而經(jīng)預(yù)處理的碳納米管長(zhǎng)度集中在數(shù)百納米到數(shù)微米之間,長(zhǎng)度相對(duì)均勻 這是碳納米管受超聲破碎、尤其在缺陷處發(fā)生斷裂所致 此外,可隱約看出原樣碳納米管管壁光滑、自然彎曲；而預(yù)處理碳納米管相對(duì)伸展、管壁粗糙,這是超聲破碎使管壁產(chǎn)生一定的缺陷、甚至在缺陷處發(fā)生斷裂所致[20,21] 預(yù)測(cè)尺寸均一、相對(duì)伸展的碳納米管更易于與液晶分子結(jié)合,便于分析碳納米管與液晶復(fù)合體系的物理參數(shù)和顯示性能,也便于評(píng)估適于與碳納米管結(jié)合的液晶所具有的結(jié)構(gòu)特點(diǎn)

圖6



圖6碳納米管的SEM圖

Fig.6Scanning electron micrograph of carbon nanotubes (a) original CNTs, (b) pretreated CNTs

3.2 電光性能測(cè)試結(jié)果和分析3.2.1 閾值電壓的測(cè)試和介電各向異性、展曲彈性常數(shù)的計(jì)算

采用圖3所示的測(cè)試方法,分別測(cè)得兩種液晶與不同比例碳納米管復(fù)合體系所灌注的平行液晶盒的C-V曲線,如圖7所示 采用切線法求得不同液晶/碳納米管復(fù)合體系所灌注平行液晶盒的閾值電壓,結(jié)果列于表1

圖7



圖7不同液晶/碳納米管復(fù)合體系的電容-電壓曲線

Fig.7Capacitance-voltage curves of different LC/CNTs composite systems

Table 1

表1

表1不同液晶/碳納米管復(fù)合體系的閾值電壓

Table 1Threshold voltages of different LC/CNTs composite systems

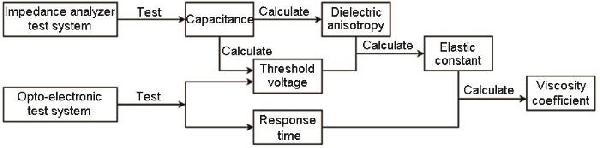
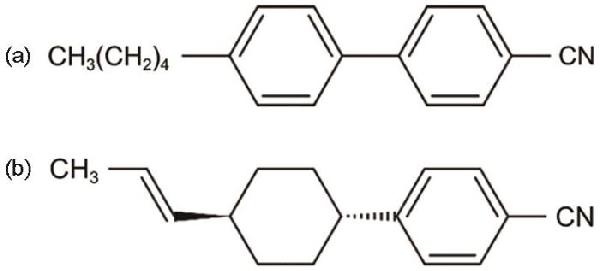
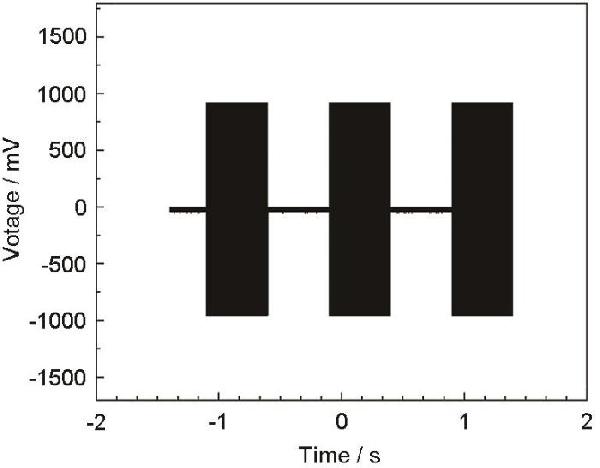
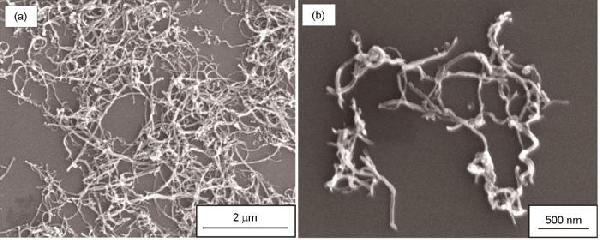
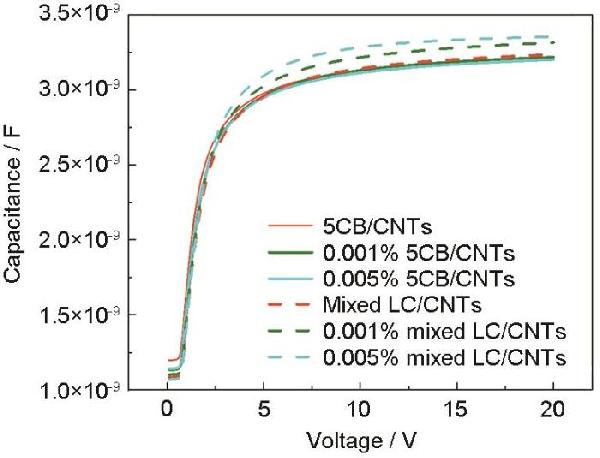
Concentration	5CB/CNTs Vth/V	Mixed LC/CNTs Vth/V
0%	0.6863	0.736
0.001%	0.7302	0.7291
Amplification	6.397%	-0.9375%
0.005%	0.7145	0.7425
Amplification	4.109%	0.8832%

由圖7可見,無(wú)論在5CB單晶還是在混晶中,摻入少量的碳納米管均使材料的電壓響應(yīng)行為改變,其改變量隨著摻雜濃度的不同而不同 閾值電壓的計(jì)算結(jié)果(表1)表明,摻雜0.001%(質(zhì)量分?jǐn)?shù))CNTs的5CB單晶比無(wú)摻雜時(shí)的閾值電壓增大了6.397%,摻雜0.001%CNTs的混晶比無(wú)摻雜時(shí)的閾值電壓降低了0.9375%,而摻雜0.005%CNTs的兩種液晶比無(wú)摻雜時(shí)的閾值電壓都有所提高 這表明,碳納米管的摻入確實(shí)影響液晶的閾值電壓,但是對(duì)液晶閾值電壓的影響不明顯 由 式(1)可知,對(duì)于平行液晶盒,閾值電壓受液晶介電各向異性和展曲彈性常數(shù)的影響 將碳納米管與液晶復(fù)合,一方面,碳納米管因固有較大的介電各向異性可能使原液晶介電各向異性的增大；另一方面,碳納米管的高長(zhǎng)徑比也可能使原液晶展曲彈性常數(shù)的增大 因此,平行液晶盒中復(fù)合體系閾值電壓的改變并不明顯

先采用雙電容法,根據(jù)測(cè)得的不同液晶/碳納米管復(fù)合體系所灌注的平行液晶盒在低電壓下的電容值和相應(yīng)垂直液晶盒在高電壓下的電容值,求得各復(fù)合體系的介電各向異性 結(jié)果列于表2 繪制不同種類液晶的介電各向異性隨摻雜濃度的變化曲線,如圖8所示

Table 2

表2

表2不同液晶/碳納米管復(fù)合體系的介電各向異性

Table 2Dielectric anisotropy of different LC/CNTs composite systems

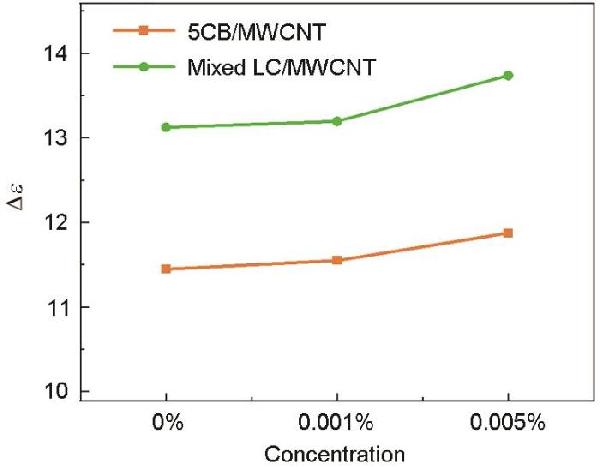
Concentration	5CB/CNTs Δε	Mixed LC/CNTs Δε
0%	11.44800577	13.12442359
0.001%	11.55039618	13.19549275
Amplification	0.894%	0.542%
0.005%	11.87458041	13.73746503
Amplification	3.726%	4.671%

圖8



圖8不同液晶/碳納米管復(fù)合體系介電各向異性隨摻雜濃度的變化

Fig.8Dielectric anisotropy curves of different LC/CNTs composites with doping concentration

由表2和圖8可見,摻入碳納米管后兩種液晶的介電各向異性均有所提高,且隨著摻雜質(zhì)量分?jǐn)?shù)的增加而增大 其原因是,碳納米管具有更大的介電各向異性,并且隨著碳納米管質(zhì)量分?jǐn)?shù)的增加其間距減小、介電各向異性提高更大 同時(shí),摻雜0.005%CNTs后,混晶的介電各向異性相對(duì)增幅為4.671%,大于5CB介電各向異性的相對(duì)增幅3.726%,意味著碳納米管的摻入對(duì)混晶介電各向異性的影響更顯著

然后使用 式(1)計(jì)算各復(fù)合體系的展曲彈性常數(shù),結(jié)果列于表3 結(jié)果表明,碳納米管的摻入使原液晶的展曲彈性常數(shù)增大 其原因是,展曲彈性常數(shù)與長(zhǎng)徑比密切相關(guān),各向異性結(jié)構(gòu)的長(zhǎng)徑比越大越難發(fā)生展曲形變,即展曲彈性常數(shù)隨著長(zhǎng)徑比的增大而增大 而碳納米管的長(zhǎng)徑比比液晶分子的大得多,因此摻入碳納米管使二者復(fù)合體系的展曲彈性常數(shù)增大

Table 3

表3

表3不同液晶/碳納米管復(fù)合體系的展曲彈性常數(shù)

Table 3Splay elastic constants of different LC/CNTs composites

Concentration	5CB/CNTs k11/N	Mixed LC/CNTs k11/N
0%	4.837×10-12	6.378×10-12
0.001%	5.525×10-12	6.293×10-12
0.005%	5.438×10-12	6.794×10-12

由此可見,摻入碳納米管增大了原液晶材料介電各向異性,也增大了材料的展曲彈性常數(shù),致使摻入碳納米管對(duì)液晶閾值電壓的影響不明顯 但是,液晶顯示器的主要能耗由背光源產(chǎn)生,且液晶驅(qū)動(dòng)系統(tǒng)的能耗很小,因此在一定程度上閾值電壓的改變對(duì)器件能耗的影響并不顯著

3.2.2 響應(yīng)時(shí)間的測(cè)試和粘滯系數(shù)的計(jì)算

使用圖4所示的光電測(cè)試系統(tǒng)分別測(cè)得兩種液晶與不同比例碳納米管復(fù)合體系所灌注的平行液晶盒的歸一化透光率隨時(shí)間的動(dòng)態(tài)變化曲線,如圖9所示,并由此求得各復(fù)合體系的響應(yīng)上升時(shí)間和響應(yīng)下降時(shí)間,分別列于表4、5 還繪制不同種類液晶的響應(yīng)時(shí)間隨摻雜濃度變化的直方圖,如圖10所示

圖9



圖9不同液晶/碳納米管復(fù)合體系的歸一化透光率隨時(shí)間的變化

Fig.9Comparison of normalized transmittance versus time curves of different LC/CNTs composites

Table 4

表4

表4不同液晶/碳納米管復(fù)合體系的響應(yīng)上升時(shí)間

Table 4Rise time of different LC/CNTs composites

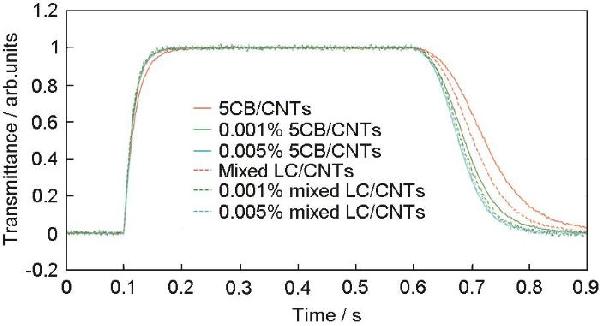
Concentration	5CB/CNTs τon/s	Mixed LC/CNTs τon/s
0%	0.1572	0.1392
0.001%	0.1206	0.0952
0.005%	0.0994	0.0996

Table 5

表5

表5不同液晶/碳納米管復(fù)合體系的響應(yīng)下降時(shí)間

Table 5Fall time of different LC/CNTs composites

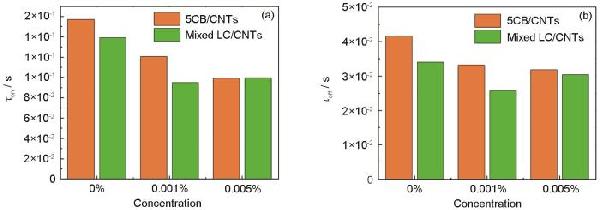
Concentration	5CB/CNTs τoff/s	Mixed LC/CNTs τoff/s
0%	0.0416	0.034
0.001%	0.0332	0.0258
0.005%	0.0318	0.0304

圖10



圖10不同液晶/碳納米管復(fù)合體系的響應(yīng)時(shí)間

Fig.10Response time of different LC/CNTs composites (a) Rise time; (b) Fall time

由表4、5可知,無(wú)論是5CB單晶還是混晶,隨著碳納米管質(zhì)量分?jǐn)?shù)的增大其響應(yīng)上升時(shí)間和下降時(shí)間都顯著降低 這表明,摻入碳納米管可提高液晶材料分子的響應(yīng)速度,縮短液晶器件的響應(yīng)時(shí)間 圖10表明,混晶響應(yīng)時(shí)間降低幅度的大于單晶,意味著碳納米管的摻入對(duì)混晶體系對(duì)外場(chǎng)的影響更加顯著

還基于 式(3)計(jì)算處各復(fù)合體系的粘滯系數(shù),列于表6 繪制的各復(fù)合體系粘滯系數(shù)隨摻入不同質(zhì)量分?jǐn)?shù)碳納米管的變化曲線,如圖11所示

Table 6

表6

表6不同液晶/碳納米管復(fù)合體系的粘滯系數(shù)

Table 6Viscosity coefficient of different LC/CNTs composites

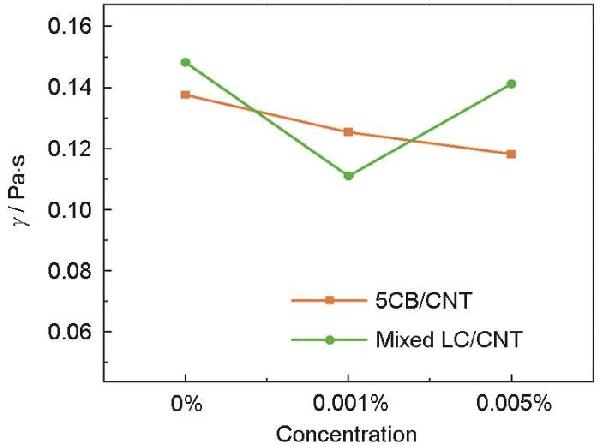
Concentration	5CB/CNTs γ/Pa?s	Mixed LC/CNTs γ/Pa?s
0%	0.138	0.1484
0.001%	0.125	0.111
Amplification	-8.848%	-25.131%
0.005%	0.118	0.141
Amplification	-14.059%	-4.751%

圖11



圖11不同液晶/碳納米管復(fù)合體系的粘滯系數(shù)隨摻雜濃度的變化

Fig.11Curves of viscosity coefficient of different LC/CNTs composites with doping concentration

由表6可見,隨著碳納米管的摻入復(fù)合體系的粘滯系數(shù)比原液晶材料的增幅為負(fù),意味著摻入碳納米管使兩種液晶的粘滯系數(shù)都明顯降低 其原因是,碳納米管管壁的多孔結(jié)構(gòu)吸附了很多液晶分子,使碳納米管附近單位體積內(nèi)液晶分子數(shù)目有所降低,從而降低了體系的粘滯系數(shù)；其原因也可能是,具有類似長(zhǎng)鏈狀結(jié)構(gòu)的碳納米管束縛其周圍液晶分子的自由運(yùn)動(dòng),從而增加了碳納米管與非束縛態(tài)液晶分子之間的距離,進(jìn)而降低了體系的粘滯系數(shù) 特別是同樣可以看到,摻入碳納米管質(zhì)量分?jǐn)?shù)為0.001%時(shí)混晶粘滯系數(shù)的降幅可高達(dá)25.131%,遠(yuǎn)大于相同條件下5CB單晶的降幅8.848% 但是,由圖11可見,隨著碳納米管質(zhì)量分?jǐn)?shù)的增加混晶的粘滯系數(shù)略有上升,這可能是體系粘滯系數(shù)越低越不容易維持碳納米管的良好分散、致使碳納米管在范德瓦爾斯作用[9]下產(chǎn)生團(tuán)聚而減小了其與非束縛態(tài)液晶分子之間的距離[10]

3.3 理論計(jì)算結(jié)果和分析

基于密度泛函理論的第一性原理,對(duì)CNT、5CB、16CN、CNT/CNT、CNT/5CB、CNT/16CN、5CB/5CB、16CN/16CN、5CB/16CN等九種體系結(jié)構(gòu)進(jìn)行幾何優(yōu)化和能量計(jì)算,所得各體系的總能量和結(jié)合能列于表7；碳納米管與液晶分子之間相互作用的穩(wěn)定模型如圖12所示；相應(yīng)的液晶分子以及碳納米管中部分原子或結(jié)構(gòu)的電荷轉(zhuǎn)移列于表8

Table 7

表7

表7各體系的總能量和結(jié)合能

Table 7Total energy and binding energy of different systems

Molecule	Total energy/kJ?mol-1	Binding energy /kJ?mol-1
CNT	-16020259.55	-
5CB	-1972813.646	-
16CN	-1772811.692	-
CNT/CNT	-32040766.04	-246.928
CNT/5CB	-17993178.59	-105.393
CNT/16CN	-17793154.91	-83.667
5CB/5CB	-3945693.537	-66.244
16CN/16CN	-3545638.782	-15.399
5CB/16CN	-3745694.349	-105.393

圖12



圖12碳納米管與液晶分子相互作用的穩(wěn)定模型

Fig.12Stable model of interaction between carbon nanotubes and liquid crystal molecules. The label started by R refers to all six carbon atoms on the benzene or cyclohexane (a) CNT/5CB, (b) CNT/16CN

Table 8

表8

表8液晶分子和碳納米管部分原子或結(jié)構(gòu)的電荷轉(zhuǎn)移量

Table 8Charge transfer of some atoms or structures in liquid crystal molecules and carbon nanotubes

Atom	CNT/5CB charge/e?atom-1	CNT/16CN charge/e?atom-1
C1	0.011	0.012
C2	-0.009	-0.011
C3	0.003	0.006
C4	0.017	0.025
N1	-0.009	-0.011
R1	0.002	-0.008
R2	0.001	-0.04
H1	0.002	0.027

由表7的能量計(jì)算結(jié)果可知,兩種液晶與碳納米管間的結(jié)合能(CNT/5CB, CNT/16CN)均大于兩液晶分子間的結(jié)合能(5CB/5CB, 16CN/16CN, 5CB/16CN)而小于兩碳納米管間的結(jié)合能(CNT/CNT),意味著分散的碳納米管可與液晶穩(wěn)定結(jié)合；電荷轉(zhuǎn)移結(jié)果表明,液晶分子5CB失去電子總數(shù)為0.011 e/mol,而液晶分子16CN失去電子總數(shù)為0.007 e/mol 這意味著碳納米管與液晶分子相互作用的親電子性,其中表8列出了液晶分子中部分原子或結(jié)構(gòu)的電荷轉(zhuǎn)移 這種親電子性使碳納米管具有一定電偶極矩,如圖12及表8所示 靠近液晶分子極性端的C4原子失去電子,而靠近液晶分子另一端的C2原子獲得電子,電荷轉(zhuǎn)移改變了碳納米管中電荷分布的對(duì)稱性；碳納米管的誘導(dǎo)偶極特性,有利于提高其與液晶分子結(jié)合的介電各向異性

同時(shí),由表8可見,液晶分子極性端的氮(N)原子獲得電子,顯示氰基具有強(qiáng)烈的吸電子效應(yīng) 由表7可見,CNT/5CB的結(jié)合能大于CNT/16CN的結(jié)合能,因?yàn)橄啾?CB的聯(lián)苯結(jié)構(gòu),16CN中的環(huán)己烷降低了其結(jié)構(gòu)的共軛性 但是,16CN環(huán)己烷中氫(H)原子與碳納米管中碳(C)原子間的最近距離為0.261 nm,介于共價(jià)鍵與范德瓦爾斯作用之間 這意味著,16CN中環(huán)己烷與碳納米管之間也可能存在較強(qiáng)的相互作用而維持體系穩(wěn)定的結(jié)合狀態(tài)；且根據(jù)表8列出的各原子電荷轉(zhuǎn)移,16CN柔軟部分的雙鍵也與碳納米管之間有相互作用 由此可見,選擇帶有較多苯環(huán)、環(huán)己烷、雙鍵等與碳納米管具有相互作用結(jié)構(gòu)的液晶分子,可增大液晶分子與碳納米管之間的結(jié)合作用,實(shí)現(xiàn)二者之間更穩(wěn)定的結(jié)合、增大介電各向異性、改善復(fù)合體系的物理參數(shù)和顯示性能

4 結(jié)論

將碳納米管分別與5CB單晶、5CB/16CN混晶進(jìn)行復(fù)合,摻入少量碳納米管可改變液晶材料的閾值電壓,增大復(fù)合體系的介電各向異性與展曲彈性常數(shù)；隨碳納米管濃度的提高單晶和混晶的介電各向異性分別提高了3.726%和4.671% 碳納米管的摻入可顯著降低液晶的粘滯系數(shù)和提高液晶的響應(yīng)速度,摻入碳納米管使上升時(shí)間和下降時(shí)間均表現(xiàn)出顯著降低的趨勢(shì),而單晶和混晶粘滯系數(shù)的降幅最高分別達(dá)到了14.059%和25.131%

碳納米管與液晶分子之間存在明顯的電荷轉(zhuǎn)移,二者的相互作用足以克服液晶分子間的結(jié)合能,將液晶分子吸附在其表面 碳納米管因吸附液晶分子產(chǎn)生電荷分布不對(duì)稱而具有一定偶極矩,有利于增大復(fù)合體系的介電各向異性與帶來(lái)場(chǎng)效應(yīng)的改變

參考文獻(xiàn)

View Option 原文順序文獻(xiàn)年度倒序文中引用次數(shù)倒序被引期刊影響因子

[1]

Boruah B R.

Dynamic manipulation of a laser beam using a liquid crystal spatial light modulator

[J]. American Journal of Physics, 2009, 77: 331

DOIURL [本文引用: 1]

[2]

Namkung J, Zou Y, Abu-Abed A, et al.

Capacitive techniques to monitor of anchoring energy for liquid crystal sensors

[J]. IEEE Sensors Journal, 2010, 10: 1479

DOIURL [本文引用: 1]

[3]

Galanis J, Nossal R, Losert W, et al.

Nematic order in small systems: measuring the elastic and wall-anchoring constants in vibrofluidized granular rods

[J]. Physical Review Letters, 2010, 105: 4

[本文引用: 1]

[4]

Sui Z M, Chen X, Wang L Y, et al.

Study on the doping and interactions of metal nanoparticles in the lyotropic liquid crystals

[J]. Acta Physico-Chimica Sinica, 2006, 22: 737

DOIURL [本文引用: 1]

[5]

Dierking I, Scalia G, Morales P.

Liquid crystal-carbon nanotube dispersions

[J]. Journal of Applied Physics, 2005, 97

[本文引用: 1]

[6]

Gorkunov M V, Osipov M A.

Mean-field theory of a nematic liquid crystal doped with anisotropic nanoparticles

[J]. Soft Matter, 2011, 7: 4348

DOIURL

[7]

Chang C R, Zhao Y, Liu Y, et al.

Liquid crystallinity of carbon nanotubes

[J]. Royal Society of Chemistry Advances, 2018, 8: 15780

[本文引用: 1]

[8]

Song W H, Kinloch I A, Windle A H.

Nematic liquid crystallinity of multiwall carbon nanotubes

[J]. Science, 2003, 302: 1363

DOIURL [本文引用: 1]

[9]

Guo Y Q, Li W J, Li X S, et al.

Influences of nickel plated multi-walled carbon-nanotube on the electro-optical properties of nematic liquid crystal

[J]. Nanotechnology, 2019, 30.

[本文引用: 2]

[10]

De Filpo G, Siprova S, Chidichimo G, et al.

Alignment of single-walled carbon nanotubes in polymer dispersed liquid crystals

[J]. Liquid Crystals, 2012, 39: 359

DOIURL [本文引用: 2]

[11]

Singh D, Singh U B, Pandey M B, et al.

Electro-optic behaviour of nematic-swcnt nanocomposites under applied bias field

[J]. Liquid Crystals, 2019, 46: 1389

DOIURL [本文引用: 2]

[12]

Lagerwall J P F, Scalia G.

Carbon nanotubes in liquid crystals

[J]. Journal of Materials Chemistry, 2008, 18: 2890

DOIURL [本文引用: 1]

[13]

Star A, Stoddart J F, Steuerman D, et al.

Preparation and properties of polymer-wrapped single-walled carbon nanotubes

[J]. Angewandte Chemie International Edition, 2001, 40: 1721

DOIURL [本文引用: 1]

[14]

Song D H, Kim J W, Kim K H, et al.

Ultrafast switching of randomly-aligned nematic liquid crystals

[J]. Optics Express, 2012, 20: 11659

DOIURL [本文引用: 1]

[15]

Jakeman E, Raynes E P.

Electro-optic response times in liquid crystals

[J]. Physics Letters A, 1972, 39: 69

DOIURL [本文引用: 1]

[16]

Tie W, Yang G H, Bhattacharyya S S, et al.

Electric-field-induced dispersion of multiwalled carbon nanotubes in nematic liquid crystal

[J]. Journal of Physical Chemistry C, 2011, 115: 21652

DOIURL [本文引用: 1]

[17]

Peterson M S E, Georgiev G, Atherton T J, et al.

Dielectric analysis of the interaction of nematic liquid crystals with carbon nanotubes

[J]. Liquid Crystals, 2018, 45: 450

DOIURL [本文引用: 1]

[18]

Ye W J, Yuan R, Dai Y Y, et al.

Improvement of image sticking in liquid crystal display doped with gamma-Fe2O3 nanoparticles

[J]. Nanomaterials, 2018, 8: 13

DOIURL [本文引用: 1]

[19]

Kaczmarek M, Dyadyusha A, Slussarenko S, et al.

The role of surface charge field in two-beam coupling in liquid crystal cells with photoconducting polymer layers

[J]. Journal of Applied Physics, 2004, 96: 2616

DOIURL [本文引用: 1]

[20]

Zuo J M, Blaha P, Schwarz K.

The theoretical charge density of silicon: experimental testing of exchange and correlation potentials

[J]. Journal of Physics: Condensed Matter, 1997, 9: 7541

DOIURL [本文引用: 2]

[21]

Diao J J, Chang C R, Zhang Z M, et al.

Reducing contact resistance of carbon nanotubes by Au doping

[J]. Chinese Journal of Materials Research, 2017, 31(7): 511

[本文引用: 1]

刁加加, 常春蕊, 張志明 等.

金摻雜降低碳納米管接觸電阻的實(shí)驗(yàn)研究

[J]. 材料研究學(xué)報(bào), 2017, 31(7): 511

DOI [本文引用: 1]

降低與金屬之間的接觸電阻是碳納米管在微納電子領(lǐng)域獲得應(yīng)用的前提,摻雜金納米粒子可有效降低碳納米管的接觸電阻 本文采用高溫焙燒在碳納米管表面構(gòu)造缺陷和親水基團(tuán),然后將碳納米管在氯金酸水溶液中超聲浸泡以吸附氯金酸,再在氫氣氣氛下加熱還原氯金酸為金 掃描電子顯微(SEM)圖片表明碳納米管被成功地?fù)诫s了金納米粒子,X射線能量散射譜(EDS)和X射線光電子譜(XPS)表明金是唯一摻雜在碳納米管上的粒子 摻雜后碳納米管的拉曼光譜中G帶波數(shù)降低說(shuō)明對(duì)碳納米管摻雜金為N型摻雜 N型摻雜劑將電子轉(zhuǎn)移給鄰近的碳原子,使碳納米管中的電子數(shù)量增加,進(jìn)而增強(qiáng)了碳納米管的導(dǎo)電性 利用介電電泳法將碳納米管組裝到一對(duì)金電極之間,并使用精密電感電容電阻(LCR)測(cè)試儀實(shí)時(shí)測(cè)量 結(jié)果表明碳納米管與金電極之間的接觸電阻較摻雜前得到了有效改善,電阻值最大可降低近50%

[22]

Wang H M, He M S, Zhang Y Y.

Carbon nanotube films: preparation and application in flexible electronics

[J]. Acta Physico-Chimica Sinica, 2019, 35: 1207

DOIURL

王灝珉, 何茂帥, 張瑩瑩.

碳納米管薄膜的制備及其在柔性電子器件中的應(yīng)用

[J]. 物理化學(xué)學(xué)報(bào), 2019, 35: 1207

Dynamic manipulation of a laser beam using a liquid crystal spatial light modulator

1

2009